假设一个深度神经网络DNN，有L层，\(\boldsymbol{a^{l}} \in\mathbb{R}^{m}\)表示第l层的输出（m为第l层神经元个数），有\(\boldsymbol{a^{l}}=\sigma(\boldsymbol{z^{l}})\)，\(\sigma\)为激活函数，激活之前的输出值\(\boldsymbol{z^{l}=w^{l}a^{l-1}+b^{l}}\)，参数矩阵\(\boldsymbol{w^{l}} \in \mathbb{R}^{dim(layer_{l}) \times dim(layer_{l-1})}\)和偏置向量\(\boldsymbol{b^{l}} \in \mathbb{R}^{layer_{l}}\)为前述线性公式的两个参数，\(w^{l}_{ji}\)表示从第l-1层第j个神经元到第l层第i个神经元的权重。

因此前向传播过程在每一层中有:

\[\boldsymbol{a^{l}=\sigma(z^{l})=\sigma(w^{l}a^{l-1}+b^{l})}\]

现在来看反向传播过程，先假设一个损失函数\(C=f(\boldsymbol{a^{L}})\)，在使用梯度下降的情况下，参数的更新通常是通过梯度的形式：

\[\boldsymbol{w^{l} = w^{l}}-\alpha \boldsymbol{ \frac{\partial{C}}{\partial{w^{l}}} \\ b^{l} = b^{l}}-\alpha \boldsymbol{ \frac{\partial{C}}{\partial{b^{l}}}}\]

其中$\alpha$表示学习率（步长）。之所以叫反向传播，是因为这里参数更新的顺序跟前向传播输出的顺序是相反的，反向传播过程中首先更新的是\(\boldsymbol{w^{L}}\)和\(\boldsymbol{b^{L}}\)，然后是\(\boldsymbol{w^{L-1}}\)和\(\boldsymbol{b^{L-1}}\)，依此类推。根据链式求导，后面所需要的梯度可以经由前面已经求出的梯度计算得出，不需要从后往前重新计算一遍，这就使得误差可以逆着网络的方向一步步“传播”回去，下面以DNN为例逐步推导出这个传播的过程。

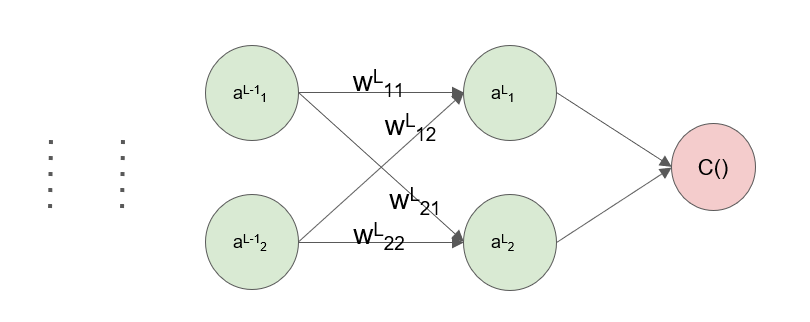
上图给出了一个简单的网络示意图，其标注与上面所述的相同。首先定义一个误差的概念，第l层的误差为\(\boldsymbol{\delta^{l}} \in \mathbb{R^{dim(layer_{l})}}\)，有\(\delta^{l}_{j}=\frac{\partial{C}}{\partial{z^{l}_{j}}}\)、\(\boldsymbol{\delta^{l}=\frac{\partial{C}}{\partial{z^{l}}}}\)，则对应的梯度可以表示为（这里其实是一笔糊涂账，只用作表示）

\[\frac{\partial{C}}{\partial{w^{l}}}=\delta^{l} \frac{\partial{z^{l}}}{\partial{w^{l}}} \\ \frac{\partial{C}}{\partial{b^{l}}}=\delta^{l} \frac{\partial{z^{l}}}{\partial{b^{l}}}\]

将上面的式子的结果化成矩阵形式就是

\[\boldsymbol{ \frac{\partial{C}}{\partial{w^{l}}}=\delta^{l}(a^{l-1})^{\top} \\ \frac{\partial{C}}{\partial{b^{l}}}=\delta^{l} }\]

下面给出\(\boldsymbol{\delta^{l}}\)的传播过程：

\[\boldsymbol{ \delta^{L}=\frac{\partial{C}}{\partial{a^{L}}} \odot \sigma^{'}(z^{L}) \\ \delta^{l}=((w^{l+1})^{\top} \delta^{l+1})\odot \sigma^{'}(z^{l}) }\]

其中$\odot$表示对应位置相乘的哈达玛积。由\(\delta^{L}_{j}=\frac{\partial{C}}{\partial{a^{L}_{j}}} \sigma^{'}(z^{L}_{j})\)可以很容易得到\(\delta^{L}\)，下面重点看一下\(\delta^{l}\)。

对于\(\boldsymbol{\delta^{l}}\)的分量，有

\[\delta^{l}_{j}=\frac{\partial{C}}{\partial{a^{l}_{j}}} \sigma^{'}(z^{l}_{j}) =\sum_{i} \frac{\partial{C}}{\partial{a^{l+1}_{i}}} \frac{\partial{a^{l+1}_{i}}}{\partial{a^{l}_{j}}} \sigma^{'}(z^{L}_{j})\]

由于

\[a^{l+1}_{i}=\sigma(\sum_{k}w^{l+1}_{ik}a^{l}_{k}+b^{l+1}_{i})\]

可以得到

\[\delta^{l}_{j}=\sum_{i} \delta^{l+1}_{i} w^{l+1}_{ij} \sigma^{'}(z^{l}_{j})\]

堆叠起来即可得到矩阵形式的\(\boldsymbol{\delta^{l}}\)。